library(tidyverse)複利計算
- 年間\(a\)万円ずつ積み立てることを考える
- 年利は\(r\)とする
\[\begin{align*} & 1年目:ar^1 \\ & 2年目:ar^1 + ar^2 \\ & 3年目:ar^1 + ar^2 + ar^3 \\ & n年目:\sum_{i=1}^{n} ar^i = \frac{ar(1 - r^n)}{1 - r} \end{align*}\]
- 等比級数の和の導出
\[\begin{align*} S =& ar + ar^2 + ar^3 + ... + ar^n \\ rS =& \qquad\; ar^2 + ar^3 + ... + ar^n + ar^{n+1} \\ S - rS =& ar - ar^{n+1} \\ S(1 - r) =& ar(1 - r^n) \\ S =& \frac{ar(1 - r^n)}{1 - r} \end{align*}\]
- シミュレーション
- \(n\):30年積み立てる
- \(a\):年間40万円ずつ(月あたり3.3333万円)
- \(r\):年利は5%と仮定
n <- 30
a <- 40
r <- 1.05
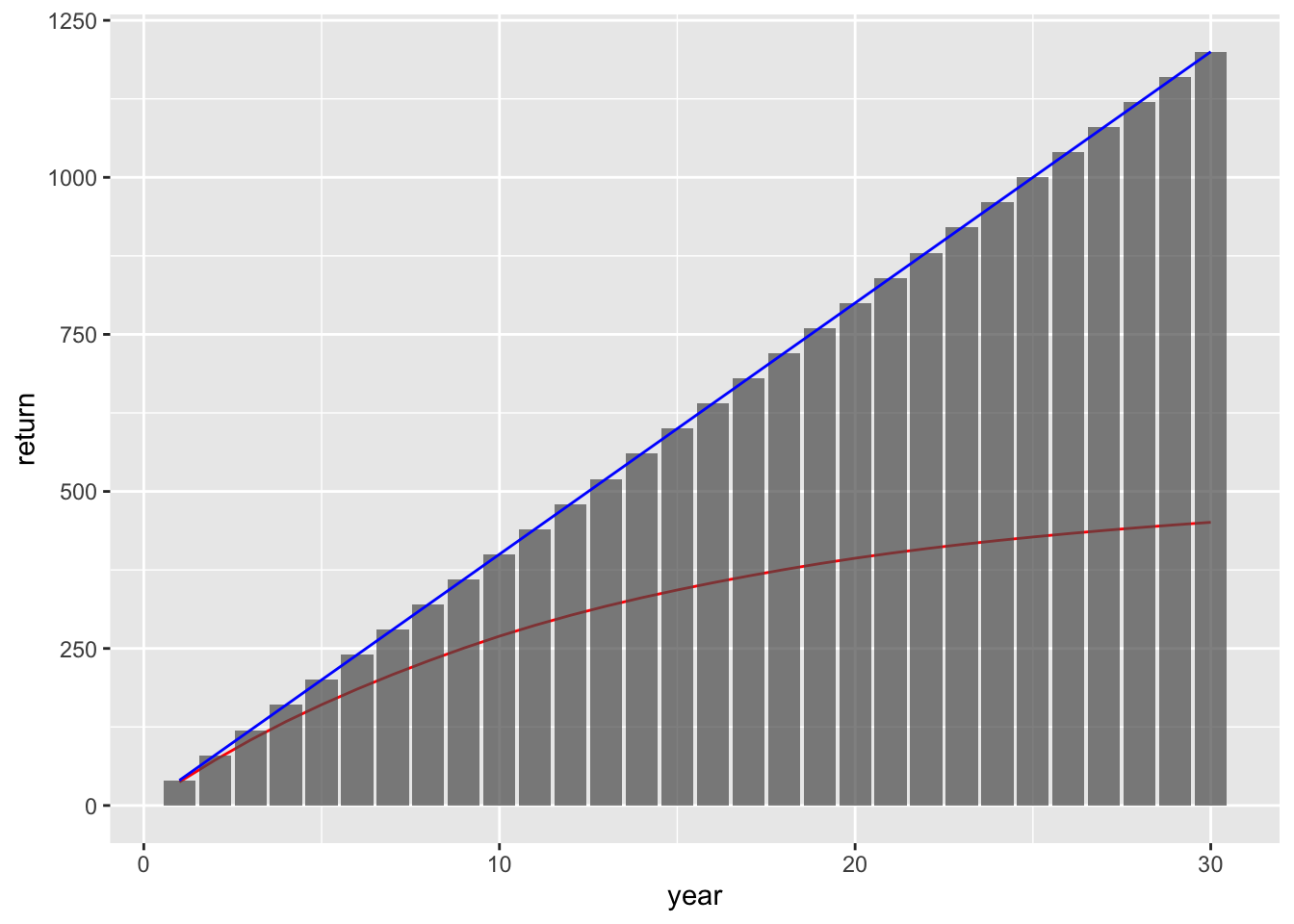
tibble(
year = 1:n,
cost = a*year,
gain = a*r^year,
return = a*r*(1 - r^year)/(1 - r),
) |>
ggplot()+
geom_line(aes(x = year, y = return), color = 'red')+
geom_col(aes(x = year, y = cost), alpha = .7)+
geom_line(aes(x = year, y = cost), color = 'blue')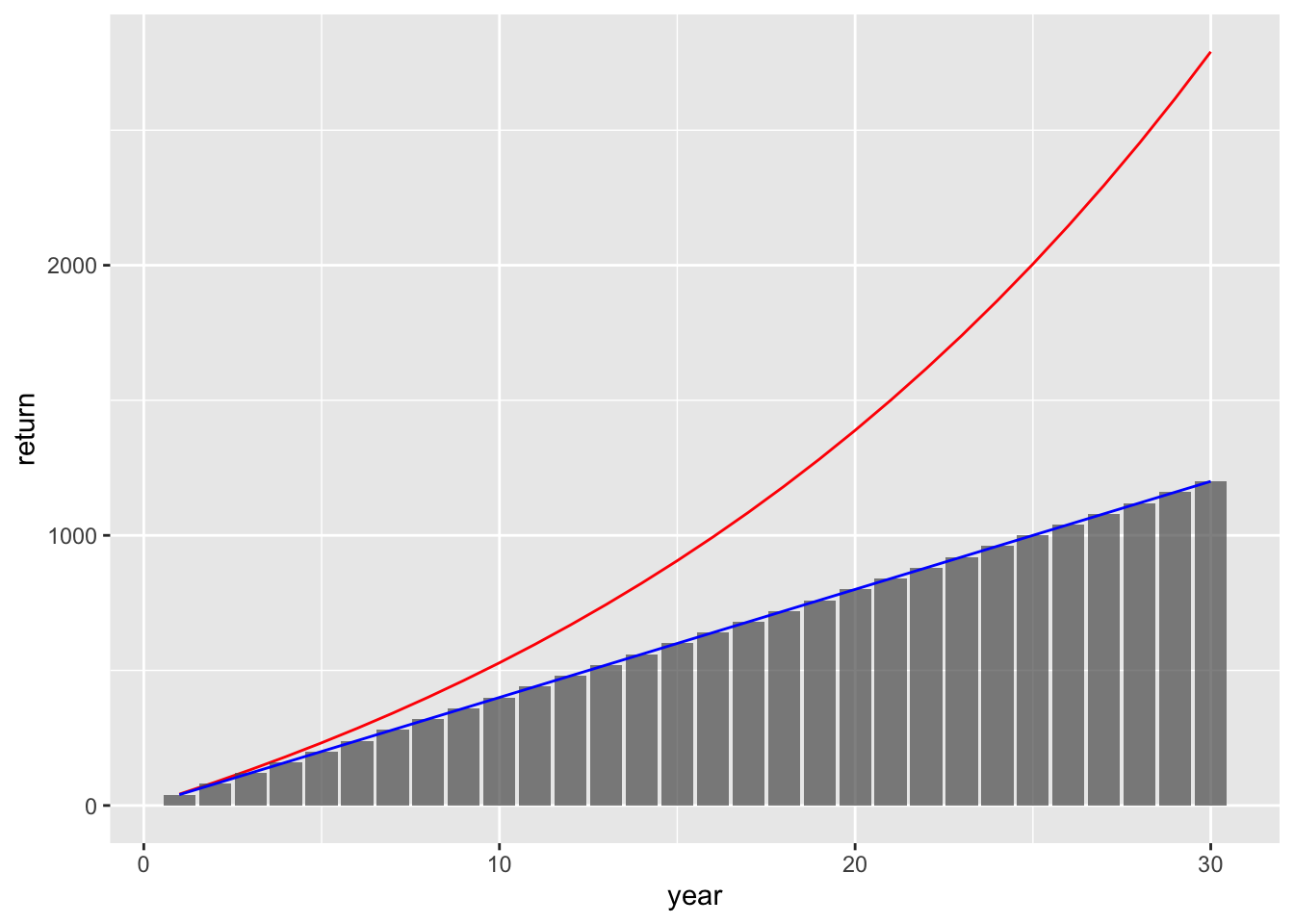
利率が年度ごとに変動する場合
- 年利は確率的に変動する値
- 定数(\(r\))ではなく、変数(\(r_i\))として考える
\[\begin{align*} & 1年目:ar_1 \\ & 2年目:ar_1 + ar_1r_2\\ & 3年目:ar_1 + ar_1r_2 + ar_1r_2r_3 = a(r_1 + r_1r_2 + r_1r_2r_3)\\ & n年目:ar_1 + ar_1r_2 + ar_1r_2r_3 + ... + ar_1r_2r_3...r_n = a\sum_{i=1}^{n} \prod_{i=1}^{n}r_i \end{align*}\]
ここで、\(r_i \sim \mathrm{Normal}(1.05, 0.1)\)とする
tibble(
year = 1:n,
rate = rnorm(n, r, .1),
cost = a*year,
return = a*(accumulate(rate, \(x, y) x*y) |> accumulate(\(x, y) x + y)),
) |>
ggplot()+
geom_line(aes(x = year, y = return), color = 'red')+
geom_col(aes(x = year, y = cost), alpha = .7)+
geom_line(aes(x = year, y = cost), color = 'blue')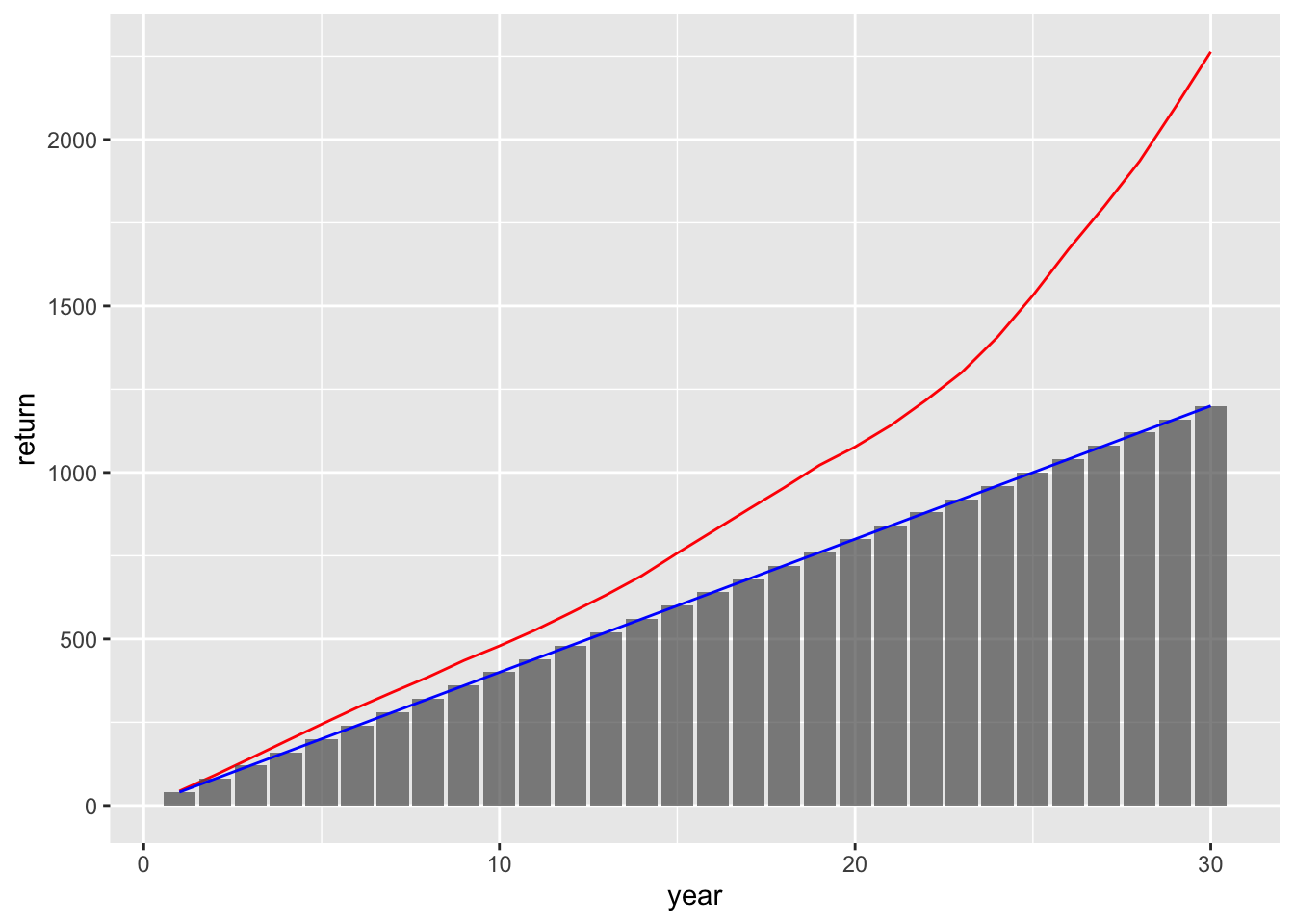
利率がランダムウォークする場合
- 景気は各時点でランダムに発生するわけではない
- むしろ1時点前の状況を強く反映する
- 年利がランダムウォークすると仮定する
\[\begin{align*} & r_1 \sim \mathrm{Normal}(1.05, 0.1) \\ & r_{i + 1} = r_i + e_i, \; e_i \sim \mathrm{Normal}(0, 0.01) \end{align*}\]
パラメータの設定が難しい…
tibble(
year = 1:n,
error = rnorm(n, 0, 0.01),
rate = accumulate(error, \(x, y) x + y, .init = rnorm(1, r, .1))[-n],
cost = a*year,
return = a*(accumulate(rate, \(x, y) x*y) |> accumulate(\(x, y) x + y)),
) |>
ggplot()+
geom_line(aes(x = year, y = return), color = 'red')+
geom_col(aes(x = year, y = cost), alpha = .7)+
geom_line(aes(x = year, y = cost), color = 'blue')